《坦克世界》用统计学方法分析白兔均伤

下面给大家带来的是《坦克世界》用统计学方法分析白兔均伤，用数据说话。

白兔的均伤为1050。

数据来源：b站各个坦克主播打白兔的实录（为了保证结果可信，故意避开了高伤集锦等偏好性明显的视频）

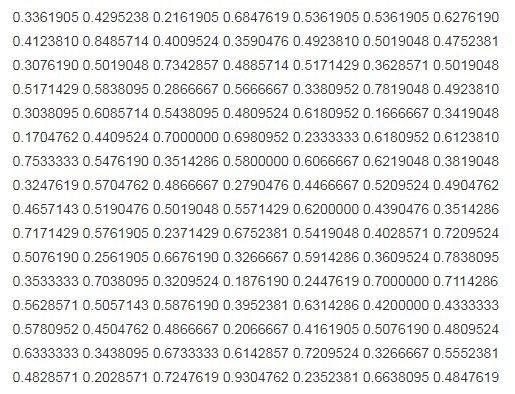
数据如下：

经常听到有人讨论，说炮弹伤害到底是正态分布还是均匀分布。我们不妨对其分布做一个检验：

首先检验是否是正态分布，使用R语言的shapiro.test函数，得到检验的p值为0.4678>0.05，我们暂时无法拒绝其服从正态分布。

然后我们再将数据进行[0,1]区间上的标准化处理，检验其是否为均匀分布，标准化后的数据如下：

我们使用Kolmogorov-Smirnov检验，检验上述数据是否服从[0,1]上的均匀分布，得到的p值为0.00003319，远小于0.05，所以我们有充足的理由相信，炮弹的伤害并不服从均匀分布。

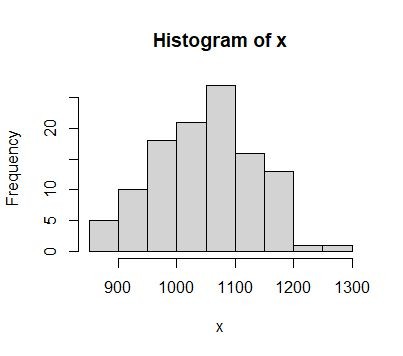
其实这一点从直方图就能看的很明显，显然不太可能是均匀分布。

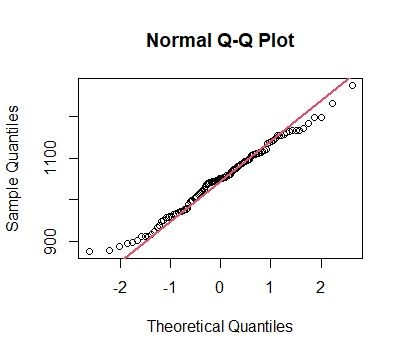
我们还可以用Q-Q图来辅助判断，根据统计学知识，如果Q-Q图中的点落在一条过原点的直线附近，那么表明数据具有很好的正态性。从Q-Q图中看，我们可以初步认为其符合正态分布。

既然我们认为数据服从正态分布，我们可以对其进行区间估计和假设检验。首先我们通过计算可以得知，均值为1048.286，方差为7152.801。

根据数理统计的知识，对其伤害的均值进行区间估计，得95%的置信区间为[1032.450 1064.121]。

我们还可以对其进行t检验，检验其均值是否为1050.

t检验的p值为0.8305>0.05，还是比较大的，不能拒绝均伤是1050这一假设，通俗来说，可以认为犯错概率不超过5%的前提下，均伤就是1050.

有吧友可能会说，wg并没有承认数据服从正态分布，好，那么我们不假设数据来自正态分布，我们也不知道炮弹伤害来自什么分布，我们可以采用非参数方法。

非参数方法有广义符号检验、Wilcoxon秩和检验和正态计分检验，其检验的目的是检验炮弹伤害的中位数是否为1050.

我们这里采用Wilcoxon秩和检验法，检验的p值为0.8972，同样也非常大，可以相信均伤为1050.

从上述检验结果来看，我们还是有比较充足的理由相信白兔的均伤为1050，尤其是大量采集样本时（大于100个），符合程度更加明显。

当然也有些不严谨的地方，因为把拿人头的伤害全都去掉了，而谁也不知道这些伤害真实值是多少。

更多相关资讯请关注：坦克世界专区